Introducing more symmetries by dressing an ultracold gas with lasers
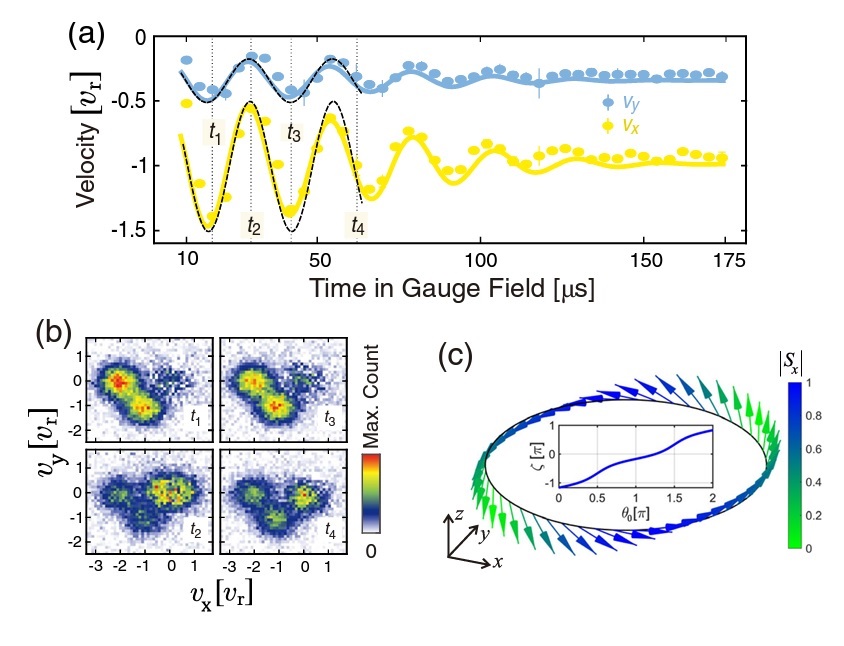
We explore quantum simulations mimicking Hamiltonians with an artificial gauge field. While most research in the ultracold atoms community focuses on lattices, to address Hubbard-like Hamiltonians for condensed-matter problems, we followed an alternative path generating gauge fields for bulk systems. Apart from its simplicity, this approach gives more diversity in gauge field structures and symmetries and allows for addressing problems ranging from quantum information to high-energy physics. The first experiment was dedicated to non-Abelian transformations to create geometrical qubits, which are known to be less prone to errors than normal qubits [1]. We then explored the matter-wave dynamic in SU(2) symmetry and found that it is governed by a non-inertial force leading to the spin-Hall effect and generalization of the Zitterbewegung relativistic effect in a two-dimensional non-Abelian gauge field [2], [3]. To create our artificial SU(2) gauge field, we suggested the so-called tripod scheme: a generalization of the celebrated Λ-scheme, used in electromagnetic-induced transparency. We extended the application domain of the tripod scheme, created an atomic Datta-Das transistor for atomtronic circuits [4], and proposed a new test of the Born rules [5]. We proposed a further extension of the tripod scheme to address SU(3) symmetry problems [6] that we are currently implementing in one of our experiments.


[1] F. Leroux, K. Pandey, R. Rebhi, F. Chevy, C. Miniatura, B. Gremaud, and D. Wilkowski, Non-Abelian and adiabatic geometric transformation in a cold atomic gas, Nature Communications 9, 3580 (2018). doi: 10.1038/s41467-018-05865-3.
[2] M. Hasan C. Madasu, K. Rathod, C. C. Kwong, C. Miniatura, F. Chevy and D. Wilkowski, Wave-packet Dynamics in Synthetic Non-Abelian Gauge Fields, Phys. Rev. Lett., 129, 130402 (2022). doi.org/10.1103/PhysRevLett.129.130402
[3] M. Hasan, C. S. Madasu, K. D. Rathod, C. C. Kwong, D. Wilkowski, Evolution of an ultracold gas in a non-Abelian gauge fields: Finite temperature effect, Q. Elec 52, 532 (2022). doi: 10.1070/QEL18071
[4] C. S. Madasu, M. Hasan, K. D. Rathod, C. C. Kwong, D. Wilkowski, Datta-Das transistor for atomtronic circuits using artificial gauge fields, Phys. Rev. R 4, 033180 (2022). doi: 10.1103/PhysRevResearch.4.033180
[5] K. S. Lee, Z. Zhuo, C. Couteau, D. Wilkowski, and T. Paterek, An atomic test of higher-order interference, Phys. Rev. A 101, 183101 (2020). doi: 10.1103/PhysRevA.101.052111.
[6] Y.-X. Hu, C. Miniatura, D. Wilkowski, and B. Grémaud, U(3) artificial gauge fields for cold atoms, Phys. Rev. A 90, 023601 (2014). doi: 10.1103/PhysRevA.90.023601.

